Jau sen vēlējos uzrakstīt par Ronnie Karsenty un citu autoru veikto pētījumu par neformālajiem matemātikas produktiem skolēniem ar zemām sekmēm, tāpēc ļoti priecājos, ka DZM nedēļas ietvaros man bija iespēja piedalīties arī dienu garā Ronnie Karsenty lekcijā. Šīs lekcijas fokuss bija radošums skolēniem ar zemām sekmēm, kur lielu nozīmi spēlē neformālie produkti.

Kas ir radošums matemātikā?

Ronnie radošumu sadalīja trīs aspektos:

• veiklība (fluency) – ideju skaits, meklējot atbildes uz uzdevumu,
• elastība (flexibility) – spēja pārslēgties starp dažādām pieejām un domāšanas veidiem viena uzdevuma ietvaros,
• oriģinalitāte (novelty) – problēmu risināšana netradicionālos veidos.

Skolēniem ar zemām sekmēm, kuriem lielākoties trūkstot veiklība un elastība matemātiskā, radošumu var veicināt, rosinot un atzīstot oriģinalitāti. Šajā sakarā viens no ieteikumiem bija atteikties no atbilžu sadalījuma pareizs / nepareizs, un pāriet uz sadalījuma produktīvs / neproduktīvs. Tādējādi atbildes, kas nav pareizas, bet kurās ir kāds domu grauds, ko var izmantot tālākā satura apguvē, kļūtu noderīgas un paceltu arī skolēnu pašapziņu.

Ronnie šo ilustrēja ar piemēru no savas pieredzes. Stundā, kur skolēni mācījās, ka lineāras izteiksmes ax+b slīpums ir koeficients pie x jeb a, kāds skolēns pajautāja, kāds ir 4x² slīpums. Skolotāja piedāvāja skolēniem šo jautājumu pārdomāt mājās, nedaudz vienkāršojot problēmu – prasot kāds ir x² slīpums. Aleksandrs piedāvāja versiju, ka tas ir x, jo x² var uzrakstīt kā x*x + 0, tāpēc koeficients pie x ir x. Šī atbilde nav pareiza, bet ir ļoti produktīva (domāju, piekritīsiet – arī radoša), jo ļāva uzsākt diskusiju par funkcijām ar mainīgiem slīpumiem.

Ko nozīmē “skolēni ar zemām sekmēm”?

Viena no lietām, kas lielākoties biedē skolēnus ar zemām sekmēm matemātikā, ir simboli. Ronnie deva arī ļoti labu ieskatu, ko nozīmē nedraudzēšanās ar simboliem.

Uzdevums: Dārzā ir n ķiršu koku. Plūmju un ķiršu koku skaits ir vienāds. Cik ir plūmju koku?

• Roberts izteica minējumu, ka n ir vienāds ar 25, jo nevarēja iedomāties neko citu, kas varētu būt šis skaitlis.
• Džila izdomāja, ka n ir 9, jo tas ir burts, ar kuru skaitlis sākas [nine].
• Emma saskaitīja, cik reižu burts ‘n’ parādās uzdevumā un pieņēma to kā n vērtību.
• Dženija zināja, ka n var būt jebkāds skaitlis, tāpēc pieņēma, ka n=1, lai aprēķini būtu vienkāršāki.

Man ir draugi, kas vidusskolas eksāmenā matemātikā saņēma A līmeni, bet saka, ka nesaprot matemātiku, jo vienīgais, ko ir darījuši, ir ņēmuši formulas un izmantojuši, bez īpašas izpratnes. Tā vien šķiet, ka arī “skolēniem ar labām sekmēm” ar matemātiku īsti neiet. Kaut kas nav labi.

Kā izpaužas radošums matemātikā skolēniem ar zemām sekmēm?

Uzdevums: aritmētiskās progresijas trešā un sestā locekļa summa ir vienāda ar 25. Piektais loceklis ir 14. Kāds ir šīs progresijas pirmais loceklis?

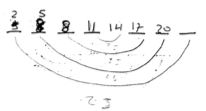Blakus ir redzama daļa no risinājuma, kādu piedāvāja skolēns, kuram, sākot mācības Ronnie programmā, paredzēja nesekmīgu zemākajā matemātikas līmeņa eksāmenā (Izraēlā ir 3 līmeņu matemātikas programmas vidusskolā). Interesanti, ka šis un citi risinājumi, kurus rādīja kā netradicionālus, man šķita daudz pieņemamāki nekā tradicionālie risinājumi ar sistēmām. Es vispār ļoti asociējos ar šiem piemēriem – es šādi risinu uzdevumus. Es šādi cenšos mācīt. Nezināju, ka ir skolotāji, kas šādus risinājumus neatzīst. Šausmas!

Bieži man šķiet, ka ir jābūt īpaši radošam, lai izdomātu tradicionālo risinājumu. Piemēram, uzdevumā “atrast divus pēc kārtas esošus skaitļus, kuru summa ir 51”, man šķistu, ka ir jābūt radošam, lai izdomātu lietot x‘us – x+x+1=51, utt. Izrādās, ka izdalīt 51 ar 2 un saprast, ka šie skaitļi ir 25 un 26 ir radošs risinājums, nevis veselais saprāts. Vēl jo trakāk – esot skolotāji, kas šādu risinājumu pārbaudes darbā nepieņem! Tā nav skolēna vaina, ka viņš/-a ir atradis/-usi vienkāršu risinājumu skolotāja uzdevumam!

Vēlarvien atceros kādu no pirmajām klasēm, kurā man lika pārstrādāt mājasdarbu, jo biju biju izdomājis un izmantoju kaut ko, ko mēs vēl nebijām mācījušies. Labi, ka manai ģimenei kaut kādu iemeslu dēļ šķita, ka man ar matemātiku viss būs kārtībā, tāpēc man bija pietiekoša pārliecība, lai šo negadījumu laistu gar ausīm un turpinātu darīt pa savam.

Kā veicināt radošumu matemātikā?

Ronnie piedāvā uzdevumus, kuriem nav vienas atbildes (izveido un atrisini vienādojumu, izmantojot 5, x, -2, -1). Pirmo reizi piekritu, tomēr vēl arvien vairāk atbalstu uzdevumus ar vienu pareizo atbildi, bet dažādiem iespējamiem risinājumiem. Viens brīnišķīgs uzdevuma piemērs, kur ir pareizā atbilde, bet arī par nepareizājām skolēni nebēdāsies un mācīsies no tām, bija šāds:

Doti skaitļi -1/6, +2, -1/2. Katru skaitli drīkst izmantot vienreiz. Drīkst izmantot darbības +, -, *, :, ( ). Jāuzraksta izteiksme, kuras rezultāts būtu pēc iespējas a) lielāks, b) mazāks, c) tuvāk 0, d) tuvāk 1, e) tuvāk 20.

Skolēniem, kuriem ar matemātiku iet grūtāk, šī ir iespēja atrast pareizo atbildi (viņiem var piedāvāt arī vienkāršāku variantu – -1, +2, +6, -3). Skolēniem, kuriem iet labi, ir iespēja pierādīt, ka viņiem ir labākā atbilde. Ja tas atbilst tēmai, šis uzdevums pat ļauj pārrunāt, vai “pēc iespējas tuvāk 1” atbildei der “1” vai tomēr nē, kas ir būtiska diskusija matemātiskajā analīzē. Šis uzdevums katram ļauj produktīvi izpausties.

Lai veicinātu radošumu, skolēnu risinājumos jāļauj un pat jāiedrošina izmantot dažādi atbilžu veidi – verbāls, ciparu, simbolisks, grafisks, vizuāls. Kā jau minēju, daudziem nepatīk simboli. Simboli ir rīks. Ja skolēni var atrast citu, viņiem piemērotāku rīku, tas viņiem būtu jāļauj. Un jāizdomā uzdevums, kur simbolu lietošana pat šiem skolēniem palīdzēs atrast risinājumu. Simboli jālieto jēgpilni.

Ronnie vienu lekciju veltīja radošumam, mācot virknes. Daži elementāri piemēri, ko var izmantot jebkurš, ir pavisam sīkas izmaiņas. Piemērs:

Uzraksti aritmētiskās progresijas pārējos locekļus. __, __, 8, 15, __, __, __

Šāds uzdevums palīdz izveidot izpratni, ka diferenci var izmantot arī atpakaļgaitā, bet šajā posmā vēl neprasa izmantot simbolisko pierakstu, kas ļauj vairāk skolēniem iesaistīties. Veidojot izpratni, nevis kaļot procedūras, krietni vienkāršāki kļūst tādi augstāka līmeņa uzdevumi kā:

Aritmētiskās progresijas pirmo divu locekļu summa un pēdējo divu locekļu summa ir 46. Pārējo locekļu summa ir 299. Cik locekļu ir šajā progresijā?

Ja ir grūtības izdomāt atbildi, var pašpikot no “skolēna ar zemām sekmēm” risinājuma.

Lasītāju aptauja: kurš no skaitļiem 15, 20, 23, 25 ir īpašs, atšķirīgs no pārējiem? Kāpēc (droši komentējiet!)?

Beigās iesaku lasāmvielu brīvam brīdim – Ronnie pētījumu par to, ko pieaugušie atceras no vidusskolas matemātikas. Pateikšu priekšā – ja viņi nav mācījušies augstākajā līmenī – neko daudz. Bet izklaidējošs pētījums.