Pagājušajā gadā matemātikas metodikas nodarbībās Jānis Mencis iedeva interesantu (man) uzdevumu – aprēķināt cos(π/5) – cos(2π/5). Šī bija brīnišķīga iespēja atgriezties skolēna ādā, jo uzdevumu varēja atrisināt ar vidusskolas pamatzināšanām, bet viegli rokās tas nedevās – man tas aizņēma vairākas stundas pāris nedēļu laikā.
Divu nedēļu darbs. Jautājums skolotājiem – ko jūs teiktu vai prasītu, ja skolēns atskrietu pie jums ar uzdevumu “Cik ir cos(π/5) – cos(2π/5)?” un manu pēdējo lapu? Jautājums skolēniem – cik ilgi jūs esat gatavi pavadīt pie viena uzdevuma?
Galerijas beigās – bonuss. Edgara, kurš šogad pabeidza maģistrus matemātikā Kembridžā, risinājums. Laiks, protams, īsāks – pusotra stunda lidmašīnā Stansteda – Rīga. Un arī tāpēc, ka vienības riņķi un ievilktus leņķus neizmanto pat tālāk mācoties matemātiku (protams, ja neizvēlas studēt klasisko ģeometriju). Un tagad savienojam vienības riņķi ar reālo dzīvi.
P.S. Man patīk vienības riņķis un ievilktie leņķi. Bet vai tas ir iemesls tos mācīt (t.i. kāds ir iemesls, kāpēc tie ir standartā?)?










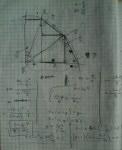

Uzdevumu var atrisināt ja zinām , ka cos36= (1+SQR(5))/4 . Lai iegūt cos 36 es apskatīju regulāro piecstūru ar malu=1.
Šo uzdevumu ir viegli atrisināt pamatskolas ģeometrijas kursa ietvaros bez trigonometrijas un pat bez kvadrātsakņu zināšanām, ja abu leņķu kosinusu vērtības vienības riņķī interpretējam kā attiecīgo nogriežņu garumus. Viss, kas šajā sakarā jāzina, ir:
a) trijstūru vienādības pazīmes;
b) vienādsānu trijstūru īpašības;
c) blakusleņķu un iekšējo šķērsleņķu īpašības;
d) trijstūra iekšējo leņķu summa.